HARd to Beat: The Overlooked Impact of Rolling Windows in the Era of Machine Learning
Francesco Audrino and Jonathan Chassot
COMPSTAT2024
August 30, 2024
Motivation
- Heteregeneous Autoregressive model is now over 15 years old.
- Well-established interpretable benchmark for realized volatility (RV) forecasting.
- Today, machine learning (ML) methods are at the center of nearly all modern research, seemingly surpassing HAR in many scenarios .
Has HAR's reign come to and end?
Our Contribution
- Demonstrate that seemingly minor modeling choices may drastically impact HAR's performance.
- Review previous works where ML outperforms HAR with and put these results into perspective.
- Study an unprecedented dataset of 1,455 U.S. stocks.
- Suggest ideal estimation approach for the HAR model.
Data
- High-frequency intraday data from Trades and Quotes (TAQ).
- 6,061 U.S. stocks the Center for Research in Security Prices (CRSP).
- ~9 years: January 1, 2015, to October 31, 2023.
- 1,455 stocks are consistently traded throughout the 9-year period.
- 27 / 30 of the Dow Jones Industrial Average (DJIA).
- 69 / 100 of the Nasdaq-100.
HAR Model
$$\mathrm{RV}_{i,t+1}^{(d)} = c + \beta^{(d)} \mathrm{RV}_{i,t}^{(d)} + \beta^{(w)}\mathrm{RV}_{i,t}^{(w)} + \beta^{(m)}\mathrm{RV}^{(m)}_{i,t} + \epsilon_{i,t+1},$$ where $\mathrm{RV}_{i,t}^{(d)}$ denotes the logarithm of the daily realized volatility of stock $i$ at time $t$ and
- $\mathrm{RV}_{i,t}^{(w)} = \frac{1}{5}\sum_{h=1}^5 \mathrm{RV}_{i,t-h+1}^{(d)}$
- $\mathrm{RV}_{i,t}^{(m)} = \frac{1}{22}\sum_{h=1}^{22} \mathrm{RV}_{i,t-h+1}^{(d)}$
HAR Model
$$\mathrm{RV}_{i,t+1}^{(d)} = c + \beta^{(d)} \mathrm{RV}_{i,t}^{(d)} + \beta^{(w)}\mathrm{RV}_{i,t}^{(w)} + \beta^{(m)}\mathrm{RV}^{(m)}_{i,t} + \epsilon_{i,t+1},$$ where $\mathrm{RV}_{i,t}^{(d)}$ denotes the logarithm of the daily realized volatility of stock $i$ at time $t$ and
- $\mathrm{RV}_{i,t}^{(w)} = \frac{1}{5}\sum_{h=1}^5 \mathrm{RV}_{i,t-h+1}^{(d)}$
- $\mathrm{RV}_{i,t}^{(m)} = \frac{1}{22}\sum_{h=1}^{22} \mathrm{RV}_{i,t-h+1}^{(d)}$
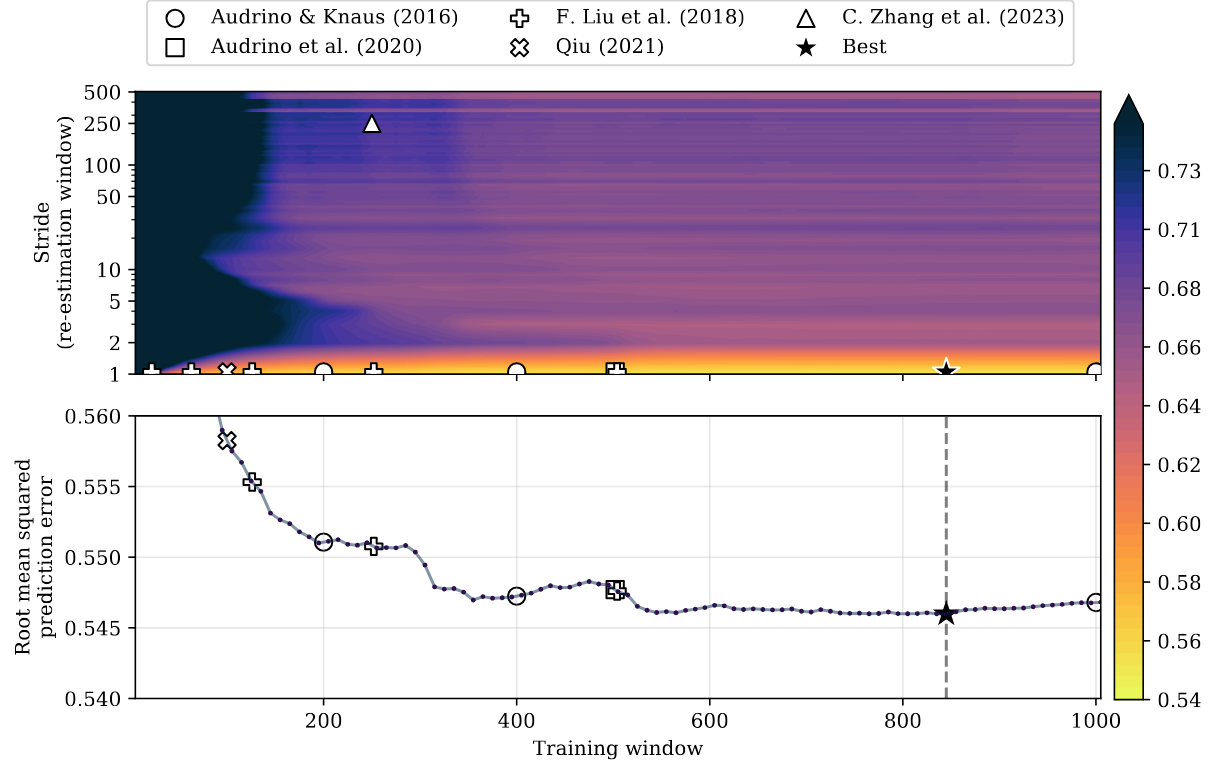
Estimating the Coefficients
Typically, HAR is estimated in a
- how often to re-fit the model (
stride orre-estimation frequency/window ) - on how much data to fit the model (
training window ) - whether to
roll orexpand the training data
Current Studies
| Study | Window Style | Training Window | Stride | Assets |
|---|---|---|---|---|
| rolling | 200, 400, 1000, 2000 | 1 | 9 | |
| rolling | 502 | 1 | 19 | |
| rolling | — | — | 29 | |
| rolling | 22, 63, 126, 252, 504 | 1 | 4 | |
| rolling | 100 | 1 | 1 | |
| expanding | 250 | 250 | 100 |
Models
HAR model
- Estimate via OLS and WLS
- Estimate individually and in a pooled manner
ML models
- Lasso
- Random Forest
- Gradient Boosted Trees
- Feedforward Neural Networks
Comparison
- Mean Squared Error (MSE), QLIKE , and Realized Utility .
- Each model is estimated once using only past RVs and once with the addition of the VIX (16 models).
- Compare distributions of the losses.
- For every asset, compute the model confidence set with a 95% level of confidence.
- Repeat the comparison for the DJIA and Nasdaq-100 universes only.
Conclusion
- A properly fitted HAR model still reigns supreme for RV forecasting.
- Use a properly fitted HAR model as benchmark when comparing your novel method…
- estimate in a
rolling manner, - re-estimate
daily , - use between
2.5 and 4 years of training data - estimate via
weighted least squares ,